Золотое сечение в рисунке и правило третей — как это применять
● Определение золотого сечения
● В чём суть золотого сечения в рисунке
● Как в рисунке быстро разделить отрезок по золотому сечению
● Правило третей
Золотое сечение, краткая справка.
Золотое сечение (золотая пропорция) — так принято называть деление отрезка на неравные части, при котором весь отрезок относится к большей части, как большая часть относится к меньшей. Другими словами, меньший отрезок так относится к большему, как больший ко всему. Короче говоря, a : b = b : с или с : Ь = b : а
Чтоб стало совсем понятно, попробуем прибавить к одному отрезку другой отрезок, а к следующему прибавлять сумму двух предыдущих. Если первый отрезок взять за единицу, то получается интересная последовательность чисел: 1+1=2; 2+1=3; 3+2=5; 5+3=8; 8+5=13; 13+8=21; 21+13=34 и тп.

Продолжая до бесконечности прибавлять суммы отрезков мы постепенно приближаемся к пропорции золотого сечения. В этой последовательности отношение большего числа к меньшему выражается иррациональным числом 1,6180339… Отношение меньшего к большему выражается числом 0,6180338…
В чём суть золотого сечения в рисунке:
Сила золотого сечения в том, что это самая асимметричная пропорция. Как говорится, ни два, ни полтора. В художественном рисунке есть известное правило: следует избегать одинаковости. Примеры пропорций которые обычно следует избегать:
1 + 1 самая скучная пропорция
1 + 2 это лучше чем 1 + 1 , но всё равно просматривается одинаковость 1+1+1
В этоху ренесанса золотое сечение называли божественной пропорцией. Во многих известных картинах композиционный центр находится примерно в точке золотого сечения, а во многих картинах и нет.
Парадокс в том, что если все пропорции в рисунке делить строго по золотому сечению, то будет совокупность одинаковых пропорций. Или, допустим, если взять десяток картин с явным композиционным центром по золотому сечению — будет выставка картин с шаблонно-однотипным приёмом композиции.
Золотое сечение — это хорошо, но не бывает универсальной пропорций на все случаи. В рисунке избегаем однообразия, стремимся к многообразию.

Как быстро разделить отрезок в пропорциях золотого сечения.
Допустим, Вы находитесь в полевых условиях, рисуете морской пейзаж. Вам захотелось линией горизонта разделить холст на небо и море в соответствии с пропорцией золотого сечения, возиться с калькулятором некогда. Делаем так: отрезок делим на восемь равных частей, после чего делаем разметку в отношении 5:3 или наоборот 3:5. В результате такого элементарного деления получается не совсем золотое сечение, но пропорция очень близкая к оному.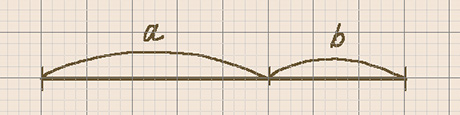
Правило третей
Что такое правило третей? — это никакое не правило, а всего лишь сетка координат, та самая сетка на экране смартфона; для удобства построения композиции кадра экран по вертикали и горизонтали разделен линиями на три части. Очевидно, что называемое правило третей противоречит правилу золотого сечения. В пропорции 1 к 3 явно просматрвается одинаковость. 1+2 это то же самое что 1+1 +1. Зато по такой сетке удобно ориентироваться, сразу видно где середина экрана и в тоже время линии не перекрывают середину, как-бы не мешают. Если от пересечения линий поставить точку чуть ближе к центру, то мы примерно попадаем в точку золотого сечения.
* * *
Богдан Бывалый
Заметки по теории и технике живописи и рисунка
